해시 (Hash)

해시란?

hash는 프랑스어 hacher [aʃe]: 썰다/다지다 에서 유래한 단어로, 잘게 다져서 요리하는 음식을 말한다. 대표적인 예로 감자를 잘게 다져서 튀김으로 만드는 해시 브라운이 있다. 이러한 문맥으로 컴퓨터 과학에서 잘게 다져 저장하는 의미로 hash라는 용어를 사용한다.

hash에서는 빠질 수 없는 Hash Function이 있는데, 이는 임의의 길이의 데이터를 고정된 길이의 데이터로 매핑하는 함수이다.
예를 들어 Java의 경우 아래와 같은 해시함수가 존재한다.

static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

Java의 내용은 관련이 없지만 설명을 위해 hashCode도 같이 보는것이 좋다.
먼저 hashCode를 얻는 방법은 아래와 같다. UTF-16의 경우 Latin-1의 상위 집합이지만, 한글과 같은 문자 때문에 필요하고 2byte 처리로 hashCode를 만든다.

public static int hashCode(byte[] value) {
    int h = 0;
    for (byte v : value) {
        h = 31 * h + (v & 0xff);
    }
    return h;
}

아무튼 일반적으로 😂이나 앨리스와 같은 값으로 해싱을 하지는 않으니, 대부분 Latin-1을 사용한다는 가정하에 설명한다.
여기서 "Alice"라는 문자열과 "Bob"이라는 문자열이 입력으로 들어온다면 다음의 과정으로 해시값을 얻을 수 있다.

1. 'A' (처음)
h = 31 * 0 + 65 = 65

2. 'l' (두번째)
h = 31 * 65 + 108
h = 2015 + 108 = 2123

3. 'i' (세번째)
h = 31 * 2123 + 105
h = 65813 + 105 = 65918

4. 'c' (네번째)
h = 31 * 65918 + 99
h = 2043458 + 99 = 2043557

5. 'e' (마지막)
h = 31 * 2043557 + 101
h = 63350267 + 101 = 63350368

결과적으로 63350368과 66965라는 해시코드가 나온다. 이 값으로 hash function을 돌리면 아래처럼 처리된다.

1) hashCode를 2진수로 변환
63350182 = 0000 0011 1110 0011 0110 1011 1000 0110

2) h >>> 16 (상위 16비트를 하위 16비트로)
0000 0000 0000 0000 0000 0011 1110 0011

3) XOR 연산 (^)
0000 0011 1110 0011 0110 1011 1000 0110  (원래 해시코드)
0000 0000 0000 0000 0000 0011 1110 0011  (>>> 16한 값)
----------------------------------------
0000 0011 1110 0011 0110 1000 0110 0101  (최종 해시값) 66063397 (십진수)

최종적으로 Alice는 66063523, Bob은 66964라는 해시값을 얻을 수 있다. 이렇게 얻어진 해시값을 통해 데이터를 저장하거나 검색할 수 있다.

해시 충돌

Java 에서는 hash 값으로 테이블 인덱스를 구할 때 (n - 1) & hash로 만든다. n은 테이블의 크기이며 초기값은 16(1 << 4)이다. Alice라는 문자열로 인덱스를 계산하면 아래와 같다.

0000 0000 0000 0000 0000 0000 0000 1111 (n - 1 = 15)
0000 0011 1111 1010 1011 0101 0000 0101 (hash: 66063397
----------------------------------------
0000 0000 0000 0000 0000 0000 0000 0101 (최종 인덱스: 5)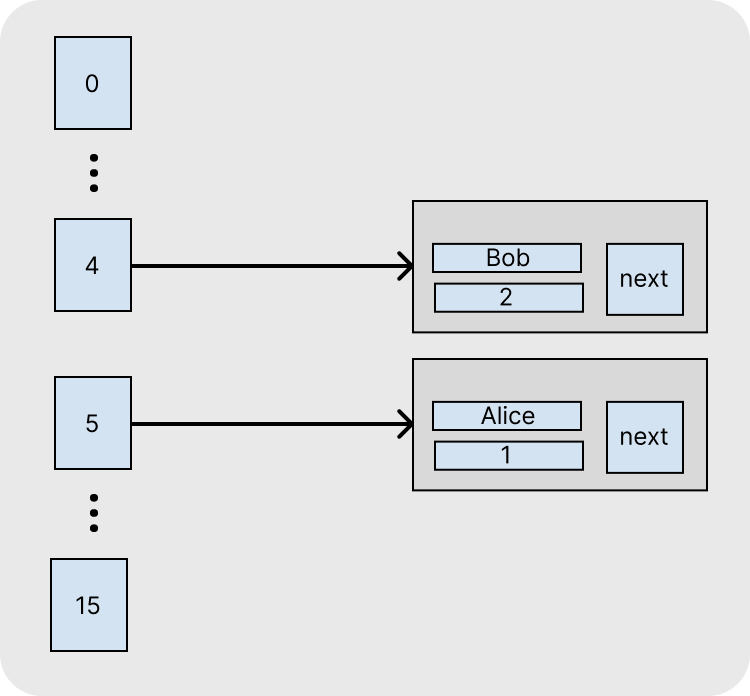

이렇게 계산된 인덱스는 현재 테이블의 크기와 해시값에 따라 생성되므로 예측하기 어려우며, 간혹 같은 인덱스를 생성하는 경우가 발생하는데, 이를 해시 충돌이라고 한다.

해시 충돌은 해시들이 어떤 계산된 값에 의해 생성된 테이블 인덱스가 같은 경우를 말한다. 해시 값이 다르더라도, 가리키는 테이블 인덱스가 같은 경우 이미 다름값이 저장이 되어있기 때문에, 충돌이 발생한다.

이런 충돌 문제를 해결하기 위해 여러가지 방법들이 고안 되었다.

해시 충돌 해결 방법

1. 체이닝

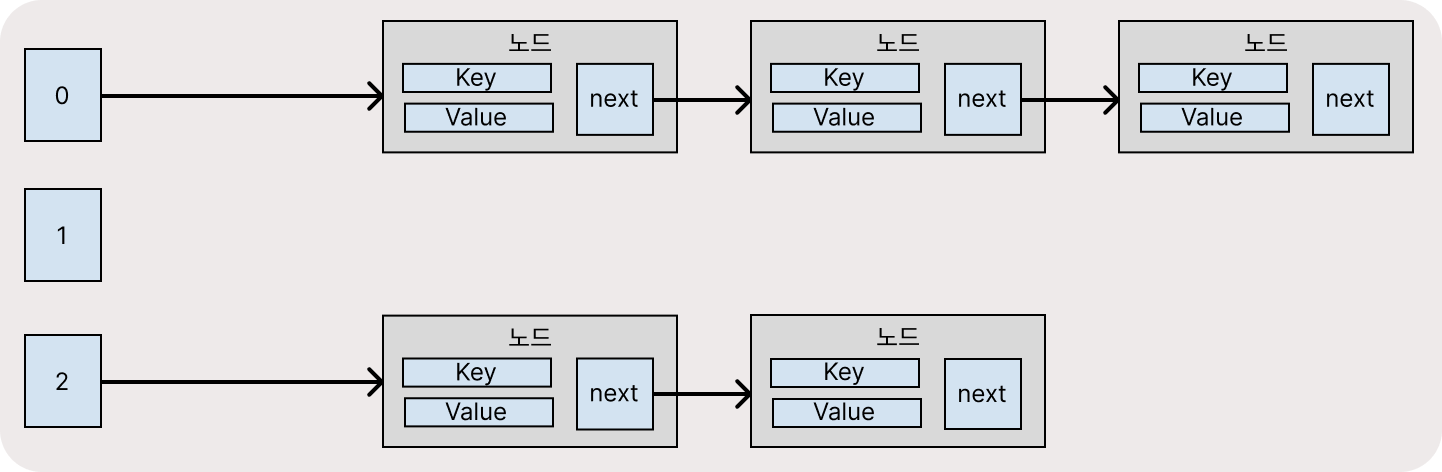
체이닝은 해시 충돌이 발생하면, 같은 테이블에 연결 리스트로 연결하는 방식이다.

해시 충돌이 자주 발생 하는것은 아니지만, 종종 발생한다. 이렇게 해시 충돌이 발생하면 해당 인덱스로 연결된 연결 리스트에서 데이터를 찾아야 한다. 같은 해시 인덱스에 대해 데이터가 저장된곳을 버킷(Bucket)이라고 하는데, 이 버킷에는 데이터가 많아질수록 성능이 저하된다.

Java의 경우 체이닝 방식을 쓰지만, 버킷의 성능을 개선하기 위해 8(threshold)개 까지는 선형 탐색을 하지만, 그 이상은 트리(Red Black) 구조로 변경하여 이진 탐색으로 성능을 향상시키며 개수가 줄어들면 다시 연결 리스트로 바꿔 선형 탐색을 한다.

2. 개방 주소법

개방 주소법은 해시 충돌이 발생할 때, 비어있는 다른 버킷을 찾아 데이터를 저장하는 방식이다. 여기서 비어있는 다른 주소에 대해 접근하는 것이기 때문에 개방 주소법이라고 하며 이 주소를 찾는 것을, 탐사(probing)이라고 한다.

개방 주소법은 체이닝과 다르게, 버킷에 한개의 정보만 저장할수 있다. 따라서 버킷이 차게 되면, 다른 버킷을 찾아 저장해야 한다. 이때 버킷은 현재 해시 인덱스와 관련이 없는 다른 버킷을 찾게된다.

개방 주소법에는 세가지 방법이 있다.

2-1. 선형 탐사

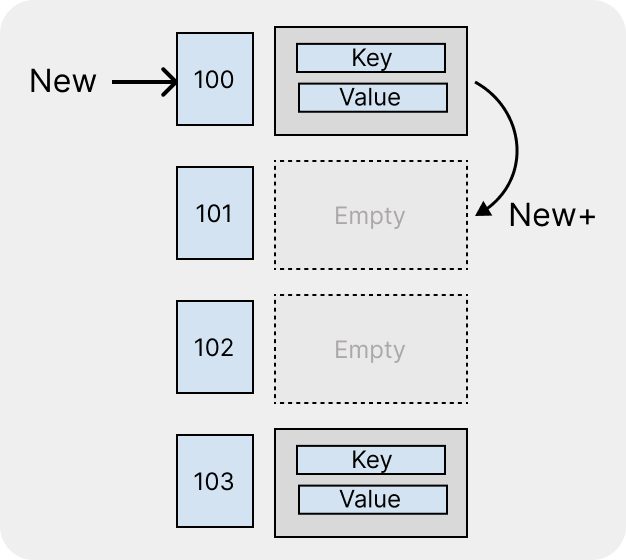
첫 번째로 선형 탐사는 해시로 계산된 인덱스가 이미 사용중이라면, 다음 인덱스로 이동하여 저장하는 방식이다. 이러한 방식은 지속적으로 다음 버킷을 찾기 때문에, 실제 해당 인덱스에 연결되어야 하는 데이터가 또 다른 버킷을 탐사해야하므로 한곳에 데이터가 모이게 된다.

이렇게 데이터가 모이는 현상을 군집화(clustering)라고 하며, 해시충돌로 다음 버킷을 계속 찾아다니는 선형 탐사는 군집화가 발생할 가능성이 높다.

2-2. 제곱 탐사 (이차 탐사)

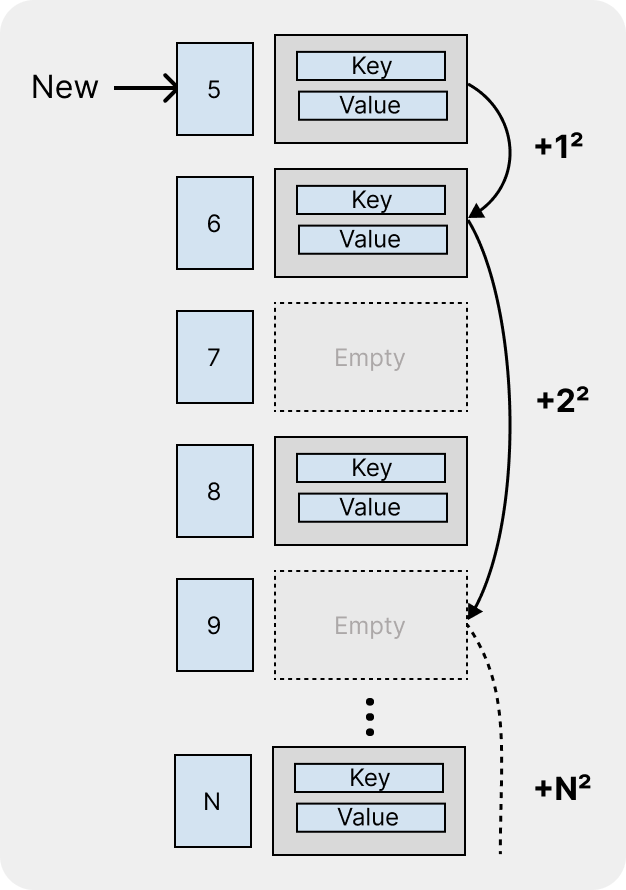
두 번째로 제곱 탐사는 선형 탐사의 군집화를 보완하기 위해 나온 기법이다. 이 기법은 N + M²(N: 원본 인덱스, M: 탐색 차수)로 다음 버킷을 찾는다.

예를 들어 다음과 위 이미지와 같이 계산된 인덱스가 5인 경우, 5번 버킷에는 이미 데이터가 있기 때문에 첫번째 탐사 인덱스로 (5 + 1² = 6)으로 이동한다.

지속적으로 버킷이 사용중이라면 아래처럼 인덱스가 계산된다.

1. 5 + 1² = 6
2. 5 + 2² = 9
3. 5 + 3² = 14
4. 5 + 4² = 21

이러한 제곱탐사는 선형탐사보다는 군집화가 적게 발생하지만, 여전히 군집화가 발생할 수 있다.

2-3. 이중 해싱

세 번째로 이중 해싱은 해싱 인덱스를 구하는 해시 함수에서 두번의 해싱으로 연산한다. 앞서 해시 함수는 해시 값을 구하는 함수라고 설명하였지만, 여기서는 해시 인덱스를 구하는 함수도 해시 함수라고 칭할 수 있다.

이중 해싱에서 해시 함수는 다음과 같다.

전체 해시 함수: h(k, i) = (h₁(k) + i * h₂(k)) % m

• h₁(k) = k % m
• h₂(k) = PRIME - (k % PRIME)

예를 들어 키값(해시 값)이 14, 테이블의 크기가 13 그리고 PRIME이 7이라고 가정한다면 아래와 같은 과정으로 인덱스를 구할 수 있다.

h~1~(14) = 14 % 13 = 1
h~2~(14) = 7 - (14 % 7) = 7 - 0 = 7

// h(14, i) = (h~1~(14) + i * h~2~(14)) % 13
i=0: (1 + 0 * 7) % 13 = 1 //첫 번째 위치
i=1: (1 + 1 * 7) % 13 = 8 //두 번째 위치
i=2: (1 + 2 * 7) % 13 = 2 //세 번째 위치

이런 식으로 테이블 크기에 맞게 적절한 분포를 할수 있다. 하지만, 이중 해싱은 선형 탐사나 제곱 탐사보다는 성능이 좋지만, PRIME을 찾는 것이 어렵다. 만약 키값(해시 값)이 23, 테이블의 크기가 10 그리고 PRIME이 7이라고 가정한다면 아래와 같은 과정으로 순환이 발생한다.

h₁(23) = 23 % 10 = 3
h₂(23) = 7 - (23 % 7) = 7 - 2 = 5

// h(23, i) = (h₁(23) + i * h₂(23)) % 10 
i=0: (3 + 0 * 5) % 10 = 3 //첫 번째 위치
i=1: (3 + 1 * 5) % 10 = 8 //두 번째 위치
i=2: (3 + 2 * 5) % 10 = 3 //세 번째 위치

3과 8인덱스에 대해 순환이 발생하며, 올바른 처리를 하지못한다. 이중해싱은 균등분포에 가장 적합하지만, 이중 해싱은 항상 두번의 해싱이 필요하며, 적절한 PRIME을 찾는 것이 어렵기 떄문에 선현 탐사나 제곱 탐사보다는 자주 사용되지 않는다.